All Games

Going Up! 3D Parkour Adventure

Boat Merge Race

Story Teller

Space Room Escape
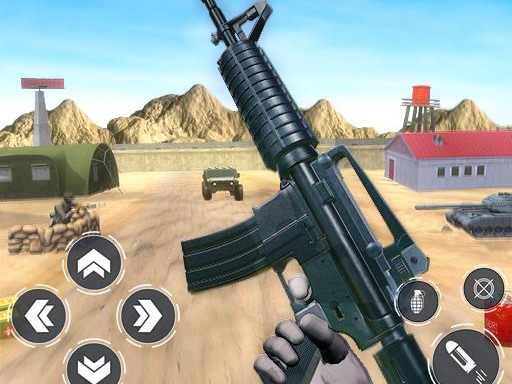
Pubg Mobile Online

Spiral Stack Rush

Draw 2 Save Puzzle

Cowboy Runners Dash

Cats: Crash Arena Turbo Stars

Vehicle Master Race

War Robots Merge

Used Car Tycoon Game

Rude Races

Monster Ruin

Coloring Games:Color Paint

Antistress Relaxation Toys Collection

Get Away Ninja

Cube Runner

Pinball Master

2 Player Games:Crazy Challenge

Car Racing 3D: Drive Mad

Bubble Shooter

Math Challenge
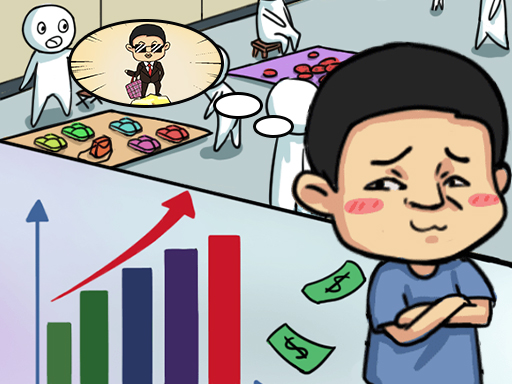
Stall Life Simulation

Build Your Home

Idle Toilet Tycoon

Flip The Bottle
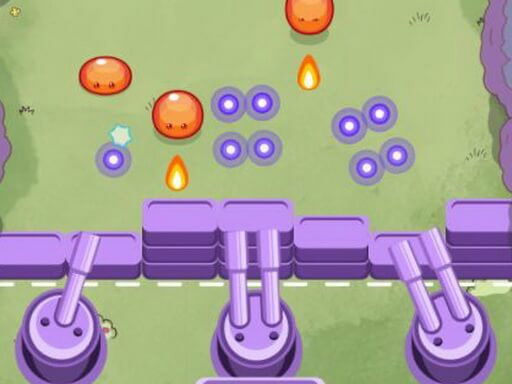
Slime Invader

Floor Is Lava

Megabot - Robot Car Transform

Spaceman Escape Adventure

Pocket Car Master

Fight For Food

Block Stair Run

Princess Halloween Boutique

Halloween Rush - Smile Tooth

Ice Scream 2: Halloween Escape

Scary Joker: Haunted Dorm

Merge Monster: Rainbow Master

Halloween Cooking

Sweet Baby Girl Halloween Fun

Halloween Salon

Halloween Coloring Games

Grimace Run

Subway Princess Run

Merge Number

Golf Field 2

War Tactics

Filled Glass 5 Fire & Ice

Wobbly Boxing

Arrow Shooter

Pinball Rush

Bubble Path

Love Doge Collect

Candy Crush

Get The Word

Play Dominoes

Coffee Break - Bubble Shooter

Tower Boom - Level Pack

Monster Blocks