इस पोस्ट में हम वृत्त के सभी फॉर्मूले ( All Circle Formula ) आपके साथ शेयर करेंगे| उम्मीद है आपको ये पोस्ट काफी पसंद आएगी| गणित से संबंधित हमारी अन्य पोस्ट पढ़ने के लिए आप दिए गए लिंक पर क्लिक करके पढ़ सकते है|
अगर आपको ये पोस्ट अच्छी लगे तो कमेंट बॉक्स में जरूर लिखें तथा अपने दोस्तों के साथ शेयर जरूर करें| इसी प्रकार की अन्य पोस्ट पढ़ने के लिए आप इस jobcutter.com वेबसाइट को फॉलो कर सकते हैं।
वृत्त किसे कहते हैं?
इसे भी पढ़ें: LCM और HCF कैसे निकालें
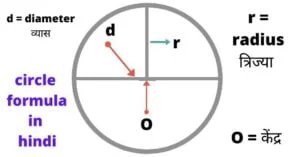
कोई भी रेखा जो vrit के केंद्र से गुजरती है और सर्कल के दो बिंदुओं को जोड़ती है, सर्कल के व्यास के रूप में जानी जाती है। त्रिज्या सर्कल के एक व्यास की आधी लंबाई है।
सर्कल का क्षेत्र सर्कल द्वारा कवर किए गए स्थान की मात्रा का वर्णन करता है और सर्कल की सीमा की लंबाई को इसकी परिधि के रूप में जाना जाता है।
r वृत्त की त्रिज्या को दर्शाता है। d वृत्त के व्यास को इंगित करता है। c वृत्त की परिधि को इंगित करता है।
वृत्त की त्रिज्या – Radius Of A Circle
वृत्त का व्यास – Vrit Ka Vyas Formula
किसी वृत्त के एक सिरे से दूसरे छोर तक की सबसे लंबी दूरी को वृत्त का व्यास ( diameter of circle ) कहा जाता है। आम तौर पर इसे “d” द्वारा दर्शाया जाता है।
इसे भी पढ़ें: संख्याओं के प्रकार एवं उनकी परिभाषा
Circle Diameter Formula
वृत्त का व्यास = 2 × त्रिज्या
d = 2 r
सर्कल का आर्क – Arc Of A Circle
यह सर्कल की परिधि का एक हिस्सा है। बड़े को प्रमुख चाप और छोटे को लघु चाप कहा जाता है।
Chord:
किसी वृत्त के भीतर का एक खंड , जो वृत्त पर दो बिंदुओं को स्पर्श करता है, वृत्त का भाग कहलाता है।
वृत्त की परिधि – Vrat Ki Paridhi
वृत्त के चारों ओर की दूरी वृत्त की परिधि या परिधि कहलाती है।
सर्कल की स्पर्शरेखा
त्रिज्या के लिए लंबवत एक रेखा जो सर्कल पर केवल एक बिंदु को छूती है।
केंद्र = O, व्यास = D और त्रिज्या = r
इसे भी पढ़ें: वर्ग ( Varg ) – परिभाषा, परिमाप तथा क्षेत्रफल
Vrit All Formula
- वृत्त का क्षेत्रफल (A) = π r 2
- वृत्त का क्षेत्रफल (A) = ( π/4 ) D2
- वृत्त का क्षेत्रफल (A) = 0.7854 D2
- वृत्त की परिधि (C) = 2 π r
- वृत्त की परिधि (C) = π D.
- वृत्त का क्षेत्रफल = (1/2) × परिधि × त्रिज्या = (1/2) × C × R
- वृत्त का व्यास (D) = √ (A / 0.7854)।
- वृत्त का व्यास (D) = 2r
Circle Formula In English
- Diameter of a Circle ( D ) = 2 × r
- Circumference of a Circle ( C ) = 2 × π × r = πd
- Area of a Circle ( A ) = π ×r 2
- Area of a Circle ( A ) = ( π/4 ) D2
- Area of a Circle ( A ) =0.7854 D2
FAQ About Vrit
Q.1. त्रिज्या किसे कहते हैं?
Ans: वृत्त की परिधि पर किसी बिंदु से वृत्त के केंद्र के बीच की दुरी त्रिज्या कहलाती है|
Q.2. परिधि किसे कहते हैं?
Ans: वृत्त के गोलाकार भाग की लम्बाई को वृत्त की परिधि कहते हैं|
Q.3. अर्धवृत्त किसे कहते हैं?
Ans: वृत्त के आधे भाग को अर्धवृत्त कहते हैं|
Q.4. वृत्तखंड किसे कहते हैं?
Ans: वृत्त की जीवा और वृत्त की चाप के बीच का क्षेत्र वृत्तखंड कहलाता है|
इसे भी पढ़ें: प्रतिशत कैसे निकाले
उम्मीद है दोस्तों आपको हमारी ये पोस्ट सर्किल फार्मूला इन हिंदी ( circle formula in hindi ) काफी पसंद आयी होगी| अगर आपका कोई प्रश्न है तो कमेंट में जरूर लिखें|
ऐसी ही अन्य पोस्ट पढ़ने के लिए बने रहे हमारे इस ब्लॉग के साथ| अपना कीमती समय देने के लिए आपका बहुत बहुत धन्यवाद|
Math vrit ki pridhi
Vrit ki pridhi or udaharn
2πr
My name is Abhishek Vishwakarma
And i like Hindi. (as you)
Vart ki tijya ka sutr
हेल्लो आनंद, वृत की त्रिज्या निकालने के लिए आपको क्षेत्रफल या परिधि या व्यास दिया होगा। आप आसानी से निकाल सकते है।
अगर क्षेत्रफल दिया है तो क्षेत्रफल को π की वैल्यू से भाग करके उसका वर्गमूल निकाल लो, अगर परिधि दी हुई है तो परिधि को 2× π के मान से भाग कर दो, अगर व्यास दिया है तो उसका आधा कर दो।
वृत्त का क्षेत्रफल (A) = 0.7854 D2 केसे हैं।
वृत्त का क्षेत्रफल (A) = 0.7854 D2 yaha 0.7854 kyo liya gya
ये वृत का क्षेत्रफल निकालने का दूसरा फार्मूला है। π और व्यास इत्यादि के मान की गणना करके इस सूत्र को बनाया गया है।
Pai ka man 3.14 hota hai
2ΠR
Nice info
Formula of antah varg ka area