नमस्कार दोस्तों Top kro में आपका स्वागत है। इस लेख में हम महत्तम समापवर्तक और लघुतम समापवर्तक ( LCM And HCF ) के बारे में पढेंगे। Lcm और Hcf गणित का महत्वपूर्ण अध्य्याय है। इस पोस्ट में आपको Hcf or Lcm के बारे में विस्तारपूर्वक जानकारी मिलेगी। इस लेख को पूरा पढ़ें ताकि आपको LCM And HCF निकालने में कोई दिक्क्त ना आये|
इस पोस्ट में आपको LCM And HCF के बारे में पूरी जानकारी जैसे :- Lcm तथा Hcf की परिभाषा, Lcm and Hcf कैसे निकालें, भिन्नों का Lcm and Hcf कैसे निकालें तथा Lcm and Hcf के महत्वपूर्ण Formulas मिलेगी। उम्मीद करता हूँ आपको हमारी इस पोस्ट के माध्यम से Hcf or Lcm के बारे में पूर्ण जानकारी मिल पाएगी।
HCF का फुल फॉर्म – HCF Ka Full Form
HCF का मतलब Highest Common Factor होता है। Hcf को हिंदी में महत्तम समापवर्तक भी कहा जाता है। जिसका अर्थ है कि सबसे बड़ा कॉमन टुकड़ा अर्थात दो या दो से अधिक संख्याओं में एक सबसे बड़ा कॉमन टुकड़ा।
इसे भी पढ़ें : वर्ग ( Varg ) – परिभाषा, परिमाप तथा क्षेत्रफल
म.स. कैसे निकालें – HCF Kaise Nikale
Hcf एक ऐसी संख्या होती है जो दो संख्याओं में कॉमन हो और दी गयी संख्याओं को भाग कर दे। ये ऐसी सबसे बड़ी संख्या होती है इससे बड़ी कोई संख्या नही होती जो दी गयी संख्याओं को भाग कर दे। अर्थात दो या दो से अधिक संख्याओ का महत्तम समापवर्तक वह बड़ी से बड़ी संख्या होती है जिससे दी गयी संख्याएं पूर्णतः विभाजित हो जाये।
उदाहरण के लिए 12, 24 तथा 30 का महत्तम समापवर्तक 6 होगा क्योंकि 6 वह बड़ी से बड़ी संख्या है जो दी गयी तीनों संख्याओं को पूर्णतः भाग कर देती है।
महत्तम समापवर्तक निकालने का तरीका – How To Find HCF
महत्तम समापवर्तक निकालने के लिए हम मुख्यत दो तरीकों का उपयोग करते हैं जिनकी मदद से हम महत्तम समापवर्तक निकाल सकते हैं। चलिए अब इन दोनों तरीकों के माध्यम से महत्तम समापवर्तक निकाल कर देखते हैं।
गुणनखंड विधि द्वारा – HCF By Prime Factorization Method
महत्तम समापवर्तक निकालने का पहला तरीका जिसका हम प्रयोग करते हैं वो है गुणनखंड विधि। इस विधि में हम दी गयी दो या दो से अधिक संख्याओ के टुकड़े कर कर लेते हैं यानी जिन छोटी से छोटी संख्याओं को आपस मे गुना करने से वह संख्या बनती हैं।
इस प्रकार सभी संख्याओं के टुकड़े निकाल लेने के बाद उन संख्याओं के टुकड़ों में जो कॉमन होता है उन्हें आपस मे गुना कर दिया जाता है। इस प्रकार हमें दो या दो से अधिक संख्याओं का महत्तम समापवर्तक मिल जाता है।
उदाहरण:- 6, 12 तथा 18 का महत्तम समापवर्तक निकालो।
उत्तर:- सबसे पहले हम दी गयी संख्याओं के छोटे से छोटे टुकड़े कर लेंगे जो अन्य किसी संख्या से भाग न हों।

6 = 2 × 3
12 = 2 × 2 × 3
18 = 2 × 3 ×3
अब हमनें तीनों संख्याओं के टुकड़े कर लिए। अब इन टुकड़ों में से जो कॉमन हो यानी तीनों संख्याओं के टुकड़ों में हो उन्हें अलग लिख लेंगे। जैसे 2 तथा 3 तीनों संख्याओ के टुकड़ों में हैं।
2 × 3 = 6
अब इन दोनों संख्याओं को आपस मे गुणा कर देंगे और हमें 6, 12 और 18 का महत्तम समापवर्तक 6 प्राप्त हुआ। 6 एक ऐसी संख्या है जो 6, 12 तथा 18 को पूर्ण रूप से भाग कर देगी तथा 6 से बड़ी ऐसी कोई संख्या नहीं है जो 6, 12 तथा 18 तीनों संख्याओं को पूर्ण रूप से भाग कर दे।
इसे भी पढ़ें : Profit And Loss
भाग विधि द्वारा – HCF By Division Method
इस विधि में हम दो या दो से अधिक संख्याओ का HCF निकाल सकते हैं। जिसमे हम संख्याओं को भाग करके उनका hcf निकालते हैं।
उदाहरण के लिए हमें 625, 775 तथा 905 का hcf निकालना है।
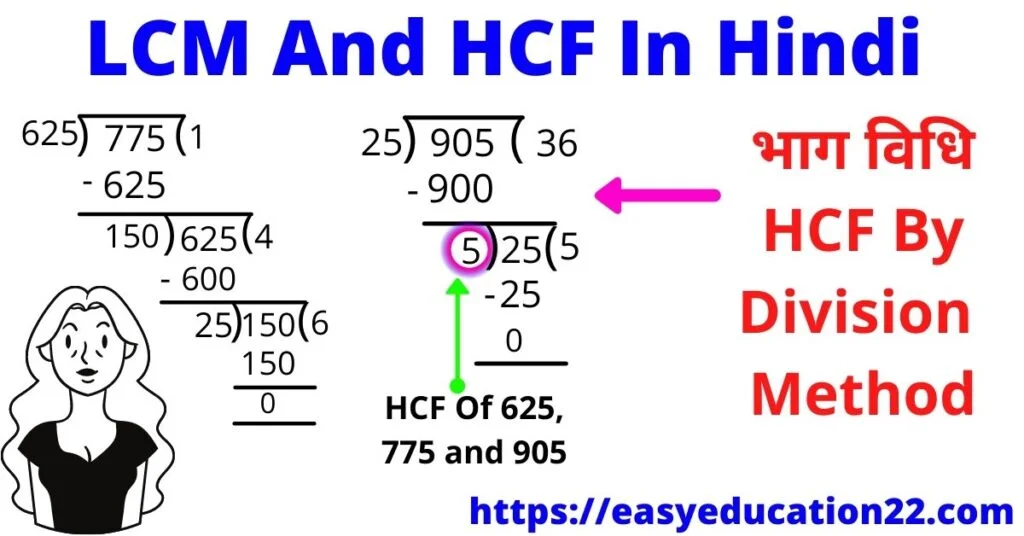
सबसे पहले हम 775 को 625 से भाग करेंगे। इसके बाद हमारे पास शेषफल 150 बच जाता है। अब हम 150 से 625 को विभाजित करेंगे तथा हमें शेषफल 25 प्राप्त हुआ। अब हम 25 से 150 को विभाजित करेंगे तथा हमारा भाग पूरा पूरा लग गया। इस विधि में हमें जब तक 0 प्राप्त नहीं होता हम भाग करते रहेंगे।
हमें अंतिम भाजक 25 प्राप्त हुआ। अब हम 905 को 25 से भाग करेंगे। हमें शेषफल 5 प्राप्त हुआ तथा इस 5 से 25 को भाग करेंगे। इस प्रकार हमें शेषफल 0 प्राप्त होगा तथा अंतिम भाजक यानी 5 हमारा HCF होगा।
LCM की फुल फॉर्म – LCM Ka Full Form
Lcm का मतलब lowest common multiple होता है। Lcm को हिंदी में लघुतम समापवर्तक कहते हैं। जिसका अर्थ है कि दो या दो से अधिक संख्याओ का सबसे छोटा कॉमन गुणक।
LCM एक ऐसी संख्या होती है जो दी गयी दो या अधिक संख्याओं से भाग हो जाये। LCM सबसे छोटा गुणक होता है। यह ऐसी सबसे छोटी संख्या होती है जो दी गयी संख्याओ से पूर्ण भाग हो जाये।
अर्थात दो या दो से अधिक संख्याओं का लघुत्तम समापवर्त्य वह न्यूनतम संख्या होती है जिसमें दी गई संख्याओं से पूर्णता भाग लग जाता है यानी वह न्यूनतम संख्या दी गई संख्याओं से पूर्णत विभाजित हो जाती है।
उदाहरण के लिए 6, 8 तथा 12 का लघुतम समापवर्तक 24 होगा क्योंकि 24 वह सबसे छोटी संख्या है जो 6, 8 तथा 12 से पूर्णतया भाग होती है। 24 से छोटी ऐसी कोई संख्या नहीं है जो इन तीनों संख्याओं से पूर्ण भाग हो।
इसे भी पढ़ें : त्रिभुज
LCM कैसे निकालें – LCM Kaise Nikale
Lcm निकालने के लिए भी हम मुख्यत दो तरीकों का उपयोग करते हैं जिनकी मदद से हम Lcm निकाल सकते हैं। चलिए अब इन दोनों तरीकों के माध्यम से Lcm निकाल कर देखते हैं।
गुणनखंड विधि द्वारा – LCM By Prime Factorization Method
LCM निकालने का पहला तरीका जिसका हम प्रयोग करते हैं वो है गुणनखंड विधि। इस विधि में हम दी गयी दो या दो से अधिक संख्याओ के टुकड़े कर कर लेते हैं यानी जिन छोटी से छोटी संख्याओं को आपस में गुना करने से वह संख्या बनती हैं।
इस प्रकार सभी संख्याओं के टुकड़े निकाल लेने के बाद उन संख्याओं के टुकड़ों में जो कॉमन होता है उन्हें गुणा में लिख दिया जाता है तथा जो टुकड़े बच जाते हैं उन्हें भी गुणा कर दिया जाता है। इस प्रकार हम दो या दो से अधिक संख्याओ का LCM निकाल सकते हैं।
उदाहरण के लिए हमें 8, 10 तथा 20 का लघुतम समापवर्तक निकालना है तो
8 = 2 × 2 × 2
10 = 2 × 5
20 = 2 × 2 ×5
LCM = 2 × 2 × 2 × 5 = 40
यहां हमनें 8, 10 तथा 20 के छोटे से छोटे टुकड़े कर लिए। इसके बाद हमनें देखा कि 2 इन तीनों संख्याओं के टुकड़ों में है तो हमनें 2 लिख दिया तथा अब दूसरी बार 2 का टुकड़ा 8 तथा 20 में है तब हमने उसे भी गुणा में लिख दिया। इसके बाद तीसरी बार 2 का टुकड़ा 8 में बच गया तो हमने उसे भी गुणा में लिख दिया। अब 5 का टुकड़ा 10 तथा 20 दोनों में है तो हमनें एक बार 5 लिख दिया। इस प्रकार हमें 8, 10 तथा 20 का LCM 40 प्राप्त हुआ।
भाग विधि द्वारा – LCM By Division Method
दो या दो से अधिक सँख्यायों का LCM निकालने के लिए हम भाग विधि का उपयोग भी करते है जिसे हम छोटी भाग विधि के नाम से भी जानते हैं। इस विधि में भाग देने की शुरुआत न्यूनतम अंको से होती है तथा कम से कम दो संख्याएं अवश्य भाग होती रहनी चाहिए।
उदाहरण के लिए हमें 18, 24 तथा 36 का Lcm ज्ञात करना है।
सबसे पहले हम 18, 24 तथा 36 को 2 से भाग देंगे क्योंकि 2 सबसे छोटी संख्या जिनसे ये संख्याएं भाग होती है। इसके बाद एक बार फिर से हम 2 से भाग करेंगे क्योंकि 12 तथा 18 अब भी 2 से भाग हो रही हैं। इसके बाद हम 3 से भाग करेंगे। इसके बाद एक बार फिर से हम 3 से भाग करेंगे।
अब 2 × 2 × 3 × 3 × 2 = 72
इस प्रकार 18, 24 तथा 36 का Lcm 72 होगा।
भिन्नों का LCM And HCF कैसे निकालें
भिन्नों का Hcf कैसे निकालें
भिन्नों का Hcf निकालने के लिए हम सूत्र का उपयोग करते हैं। दो या दो से अधिक भिन्नों का Hcf निकालने के लिए हम भिन्नों के अंशों का Hcf निकालेंगे तथा भिन्नों के हर का Lcm निकालेंगे। इस प्रकार प्राप्त भिन्न दी गयी भिन्नों का Hcf होगा।
भिन्नों का Lcm कैसे निकालें
भिन्नों का Lcm निकालने के लिए हम सूत्र का उपयोग करते हैं। दो या दो से अधिक भिन्नों का Lcm निकालने के लिए हम भिन्नों के अंशों का Lcm निकालेंगे तथा भिन्नों के हर का Hcf निकालेंगे। इस प्रकार प्राप्त भिन्न दी गयी भिन्नों का Lcm होगा।
इसे भी पढ़ें : Percentage
HCF और LCM के महत्वपूर्ण सूत्र | LCM And HCF Formula in Hindi
- ल.स. = (पहली संख्या × दूसरी संख्या) ÷ HCF
- ल.स × म.स. = पहली संख्या × दूसरी संख्या
- पहली संख्या = (LCM × HCF) ÷ दूसरी संख्या
- म.स. = (पहली संख्या × दूसरी संख्या) ÷ LCM
- दूसरी संख्या = (LCM × HCF) ÷ पहली संख्या
LCM एवं HCF के याद रखने योग्य तथ्य – LCM and HCF in Hindi
- दो या दो से अधिक संख्याओं का लघुत्तम समापवर्तक उन सँख्यायों से छोटा नहीं होता है।
- दो या दो से अधिक संख्याओं का महत्तम समापवर्तक उन सँख्यायों से बड़ा नहीं होता है।
- सह-अभाज्य संख्या का महत्तम समापवर्तक सदैव 1 होता है।
- दो या दो से अधिक अभाज्य संख्याओं का महत्तम समापवर्तक हमेशा 1 होता है।
- यदि एक संख्या, दूसरी संख्या का गुणज हो तो उनका लघुत्तम समापवर्तक सबसे बड़ी संख्या होती है तथा महत्तम समापवर्तक सबसे छोटी संख्या होती है।
- दो संख्याओं का महत्तम समापवर्तक अगर 1 हो तो उनका लघुत्तम समापवर्तक उन सँख्याओ का गुणनफल होता है।
आशा करता हूँ दोस्तों आपको हमारे इस लेख के माध्यम से LCM And HCF के बारे में महत्वपूर्ण जानकारियां पूर्ण रूप से मिल पाई होंगी। इस पोस्ट को पूरा पढ़ने के बाद आपको LCM And HCF में किसी प्रकार की दिक्क्त नहीं आएगी|
उम्मीद है इस लेख Lcm and Hcf में दी गयी जानकारी को समझने में आपको किसी प्रकार की समस्या नही हुई होगी। LCM And HCF गणित का एक प्रमुख अध्याय है|
हमनें इस पोस्ट Lcm and Hcf में आसान भाषा का प्रयोग करने की कोशिश की है और मुझे विश्वास है की आपको अब LCM And HCF निकालने में कोई दिक्क्त नहीं होगी|
अगर आपके मन मे किसी प्रकार का कोई प्रशन है तो आप निसंकोच हमें कमेंट बॉक्स के माध्यम से लिख सकते हैं। आपके प्रशन का उत्तर जल्द से जल्द देने की कोशिश की जाएगी। अपना कीमती समय देने के लिए आपका बहुत – बहुत धन्यवाद।
बहुत अच्छा
Thanks
Apka method bahut achchha laga👌👌👌👌
Thanks Amit Kumar
Sir mera 17 August ko cuet ka paper hai aap thoda bata do kesa aayega paper please sir 🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻🙏🏻
Paper jyada mushkil nhi aata. Bs aap dhyan se hr question ko pdhen. Agr aapne acchi tyari ki h to aap jrur clear kr lengi.
You’ve worked hard for this exam, so give your best effort! Best wishes to you.
Mera vi cuet ka exam tha aap kaha se hay