इस पोस्ट में हम Shanku In Hindi के बारे में विस्तारपूर्वक जानकारी प्राप्त करेंगे। इस पोस्ट के माध्यम से आप शंकु के पूर्ण पृष्ठीय क्षेत्रफल, शंकु के वक्र पृष्ठिय क्षेत्रफल, शंकु की ऊंचाई तथा शंकु के आयतन के बारे में जान पाएंगे।
मुझे पूरा विश्वास है कि इस पोस्ट को पूरा पढ़ने के बाद आपको शंकु के प्रश्नों को हल करने में किसी प्रकार की कोई दिक्कत नहीं होंगी। इसलिए आपसे निवेदन है कि कृपया इस पोस्ट को अंत तक पूरा पढ़ें ताकि आपको किसी प्रकार की कोई परेशानी ना आये।
शंकु की परिभाषा – Shanku Ki Paribhasha
शंकु (Cone) एक ऐसी त्रिआयामी (3d) आकृति है जिसका जिसका आधार गोलाकार होता है तथा जिसका शीर्ष एक बिंदु होता है। यदि किसी Shanku का आधार एक वृत्त हो तो उसे हम लम्ब वृत्तीय शंकु कहते है। यह शंकु समान आधार और ऊंचाई वाले बेलन के 1/3 भाग के बराबर होता है।
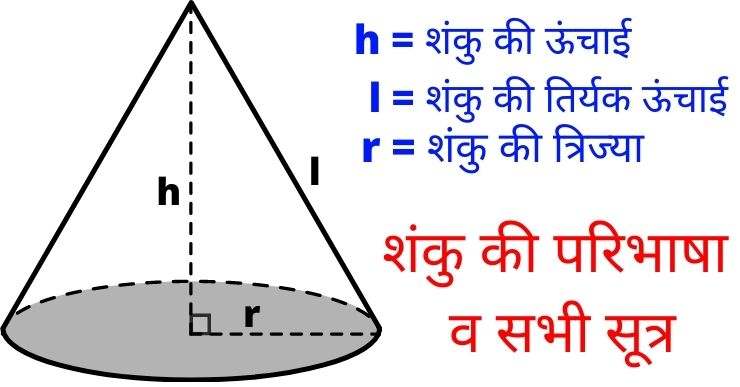
एक शंकु में केवल एक आधार होता है एवं गोलाकार होता है। यह Cone का नीचे का हिस्सा होता है। इसे शंकु का फलक भी कहा जाता है।
शंकु का शीर्ष – Shanku Ka Top
एक शंकु में एक शीर्ष होता है। शंकु का शीर्ष एक बिंदु होता है।
एक शंकु की चौड़ाई उसके गोलाकार फलक का व्यास होता है अर्थात शंकु के गोलाकार भाग का व्यास ही शंकु की चौड़ाई होती है।
इसे भी पढ़ें: BODMAS Rule In Hindi
शंकु का क्षेत्रफल – Shanku Ka Kshetrafal
अब हम Cone Ke Kshetrafal के बारे में बात करेंगे। हम Shanku Ka Area निकालने के लिए सूत्रों का उपयोग करते हैं। शंकु का क्षेत्रफल हम बहुत आसानी से निकाल सकते हैं।
शंकु का क्षेत्रफल दो प्रकार का होता है एक पूर्ण पृष्ठीय क्षेत्रफल तथा दूसरा वक्र पृष्ठीय क्षेत्रफल। आइये अब Shanku के क्षेत्रफल को निकालने के लिए महत्वपूर्ण सूत्रों को जाने।
शंकु का वक्र पृष्ठीय क्षेत्रफल – Shanku Ka Vakra Prasthiy Kshetrafal
शंकु का वक्र पृष्ठीय क्षेत्रफल निकालने के लिए हमें शंकु की त्रिज्या तथा शंकु की तिर्यक ( तिरछी ) ऊंचाई का पता होना चाहिए। तभी हम शंकु का वक्र पृष्ठीय क्षेत्रफल निकाल सकते हैं।
शंकु का वक्र पृष्ठिय क्षेत्रफल = πRL
अगर हमें शंकु का वक्र पृष्ठीय क्षेत्रफल तथा त्रिज्या दी गयी हो तो हम शंकु की तिर्यक ऊंचाई निकाल सकते हैं। इसके लिए हम शंकु के वक्र पृष्ठीय क्षेत्रफल को इसके सूत्र के बराबर लिख कर और थोड़ी सी कैल्कुलेशन करके मान ज्ञात कर सकते हैं। ऐसा ही हम अन्य सूत्रों के साथ भी कर सकते हैं।
इसे भी पढ़ें: LCM और HCF कैसे निकालें?
शंकु के पूर्ण पृष्ठीय क्षेत्रफल
शंकु का पूर्ण पृष्ठीय क्षेत्रफल निकालने का मतलब होता है शंकु के चारों तरफ का क्षेत्रफल। इसमे शंकु के तल में मौजूद वृत का क्षेत्रफल भी शामिल होता है। शंकु का पूर्ण पृष्ठीय क्षेत्रफल निकालने के लिए हम सूत्र का उपयोग करते हैं। Cone के पूर्ण पृष्ठीय क्षेत्रफल में हम शंकु तथा वृत के क्षेत्रफल को जोड़ देते हैं। क्योंकि Shanku के तल में वृत भी होता है।
जब हम शंकु के वक्र पृष्ठीय क्षेत्रफल में वृत्त का क्षेत्रफल भी जोड़ देते हैं तो हमें शंकु का पूर्ण पृष्ठीय या सम्पूर्ण पृष्ठीय क्षेत्रफल प्राप्त होता है।
शंकु के वक्र पृष्ठ का क्षेत्रफल + वृत्त का क्षेत्रफल = शंकु का पूर्ण पृष्ठीय क्षेत्रफल
अन्तः शंकु का पूर्ण पृष्ठीय क्षेत्रफल = πr ( l + r )
यहाँ R या r का मतलब शंकु के आधार की त्रिज्या होता है तथा L या l का मतलब शंकु की तिर्यक अर्थात तिरछी ऊंचाई होता है। पाई का मान हम 22/7 या 3.14 लेते हैं।
अगर किसी सवाल या प्रश्न में हमें शंकु का पृष्ठीय क्षेत्रफल निकालने के लिए कहा जाए तो हम शंकु का पूर्ण पृष्ठीय क्षेत्रफल निकालेंगे ना कि वक्र पृष्ठीय क्षेत्रफल।
इसे भी पढ़ें: वर्ग – परिभाषा, परिमाप तथा क्षेत्रफल
शंकु की तिर्यक ऊंचाई – Shanku Ki Tiryak Unchai
एक शंकु की तिर्यक ऊंचाई अर्थात तिरछी ऊंचाई को हम L या l से चिह्नित करते हैं। शंकु की तिर्यक ऊंचाई निकालने के लिए हमें शंकु का आधार तथा शंकु की तिर्यक ऊंचाई पता होनी चाहिए।
जहाँ r शंकु के आधार की त्रिज्या होती है एवं h शंकु की ऊंचाई होती है। शंकु की तिर्यक ऊंचाई हम पाइथागोरस प्रमेय से पता कर सकते हैं क्योंकि शंकु के अंदर एक समकोण त्रिभुज बनती है।
इस सूत्र के माध्यम से हम शंकु की ऊंचाई तथा त्रिज्या भी ज्ञात कर सकते हैं। बस हमें इन तीन चीजों में से किसी दो की जानकारी होनी चाहिए तब हम तीसरे का मान निकाल सकते हैं। अगर हमें Shanku की तिर्यक ऊंचाई तथा ऊंचाई का पता हो तो हम शंकु की त्रिज्या निकाल सकते हैं।
अगर हमें शंकु की तिर्यक ऊंचाई तथा शंकु की त्रिज्या का पता हो तो हम शंकु की ऊंचाई ज्ञात कर सकते हैं। बस आपको दिया गया मान इस सूत्र में रखना है और हल करना है।
इसे भी पढ़ें: Profit And Loss Formula In Hindi
शंकु का आयतन – Shanku Ka Aaytan
शंकु की बनावट के आधार पर हम Shanku का आयतन शंकु के समान आधार वाले एक बेलन के आयतन का तीसरा हिस्सा मानते हैं। जितना समान आधार वाले बेलन का आयतन होगा उसका तीसरा हिस्सा उसी आधार वाले शंकु का आयतन होगा।
शंकु का आयतन = 1/3 × बेलन का आयतन
इस प्रकार से Shanku का आयतन बेलन के आयतन का तीसरा हिस्सा होगा। इसलिए हम बेलन के आयतन को 3 से भाग कर देते हैं और हमें शंकु के आयतन का सूत्र मिल जाएगा।
इसे भी पढ़ें: त्रिभुज के प्रकार एवं सूत्र
Shanku Ke Udaharan
अब हम कुछ उदाहरणों के माध्यम से शंकु के कुछ प्रश्नों को हल करेंगे ताकि आपको शंकु के बारे में अच्छे से जानकारी मिल सके।
आप ऐसे ही कुछ अन्य सवाल खुद करके देखें। हमें उम्मीद ही नहीं पूरा भरोसा है कि इस पोस्ट को पढ़ने के बाद आप आसानी से शंकु के प्रश्नों को हल कर पाएंगे।
उदाहरण 1: एक शंकु जिसके आधार की त्रिज्या 20 cm है तथा शंकु की तिर्यक ऊंचाई 40 cm है। इस शंकु का पृष्ठीय क्षेत्रफल ज्ञात कीजिये।
हल: इस प्रश्न में हमें शंकु की त्रिज्या तथा शंकु की तिर्यक ऊंचाई दी गयी है। इसके माध्यम से हम शंकु का पूर्ण पृष्ठीय क्षेत्रफल आसानी से निकाल सकते हैं। प्रश्न में हमें पृष्ठीय क्षेत्रफल निकालने के लिए कहा गया है तो हम शंकु का पूर्ण पृष्ठीय क्षेत्रफल निकलेंगे।
शंकु के पूर्ण पृष्ठीय क्षेत्रफल का सूत्र = πr (l+r)
अब हम π की जगह 22/7 रखेंगे तथा शंकु की त्रिज्या ओर तिर्यक ऊंचाई भी रख देंगे।
= 22/7 × 20 (40 + 20)
= 3771.42 cm2
तो देखा दोस्तों आपने कितना आसान है। चलिए अब एक और उदाहरण के माध्यम से हम शंकु के बारे में कुछ और प्रश्न देखते हैं।
उदाहरण:2 एक शंकु जिसके आधार की त्रिज्या 30 cm है तथा शंकु की तिर्यक ऊंचाई 63 cm है। शंकु की ऊंचाई 42 cm है। इस शंकु का वक्र पृष्ठीय क्षेत्रफल तथा आयतन ज्ञात कीजिये।
हल: सबसे पहले हम शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात करेंगे।
शंकु के वक्र पृष्ठीय क्षेत्रफल का सूत्र = πrl
= 22/7 × 30 × 63
= 5940 cm2
अब हम शंकु का आयतन निकाल लेते हैं।
अब हम फॉर्मूले में सभी वैल्यू रख देते हैं। ध्यान रहे यहां सूत्र में त्रिज्या का वर्ग है यानी हमें त्रिज्या को 2 बार लिखना पड़ेगा।
= 1/3 × 22/7 × 30 × 30 × 42
= 39600 cm3
किसी भी वस्तु का आयतन लिखते समय उसके साथ लगी इकाई में घन लिखते हैं अर्थात उसकी घात 3 लिखते हैं और किसी भी वस्तु के क्षेत्रफल में घात 2 लिखते हैं अर्थात वर्ग लिखते हैं।
इसे भी पढ़ें: प्रतिशत कैसे निकाले?
उदाहरण: 3 एक शंकु के आधार की त्रिज्या 6 cm है तथा शंकु की ऊंचाई 8 cm है तो शंकु की तिर्यक ऊंचाई ज्ञात करो।
हल: इस प्रशन में हमें शंकु की तिर्यक ऊंचाई ज्ञात करनी है। अब हम इसमे पाइथागोरस प्रमेय का प्रयोग करेंगे।
शंकु की तिर्यक ऊंचाई का सूत्र :-
यहां l शंकु की तिर्यक ऊंचाई, r शंकु की त्रिज्या तथा h शंकु की ऊंचाई है।
अब हमें l का वर्ग बराबर 100 प्राप्त हुआ। अब हम l के वर्ग को बराबर के दूसरी तरफ लेकर जाएंगे तथा बराबर के उस पार जाते ही वर्ग, वर्ग रुट में बदल जायेगा।
l = √100
l = 10
100 का वर्गरूट 10 होता है अर्थात हमें शंकु की ऊंचाई 10 प्राप्त हुई।
अभ्यास के लिए Shanku Ke Question
अभ्यास के लिए दिए गए इन प्रश्नों का उत्तर आप हमें कमेंट बॉक्स में जरूर लिखें।
- एक शंकु की त्रिज्या 35 cm तथा तिर्यक ऊँचाई 42 cm है। इस शंकु का वक्र पृष्ठीय तथा सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात करो?
- एक शंकु कि त्रिज्या 9 cm तथा तिर्यक ऊंचाई 15 cm है। इस Shanku की ऊंचाई ज्ञात करो?
- एक शंकु की त्रिज्या 21 cm है तथा शंकु की ऊंचाई 35 cm है। इस शंकु का आयतन तथा तिर्यक ऊंचाई ज्ञात करो?
इसे भी पढ़ें: वृत्त के सभी सूत्र
Shanku FAQ
Q.1. शंकु की परिभाषा क्या है?
Q.2. शंकु के पृष्ठीय क्षेत्रफल का सूत्र क्या होता है?
Q.3. शंकु के आयतन का सूत्र बताओ?
Q.4. शंकु में कितने किनारे होते हैं?
इसे भी पढ़ें: आयत ( Rectangle )
उम्मीद करता हूँ दोस्तों इस पोस्ट के माध्यम से आपको Shanku के बारे में पूर्ण जानकारी मिल पाएगी। हमने इस लेख में शंकु के बारे में बहुत आसान भाषा मे लिखने का प्रयत्न किया है।
मुझे पूरा विश्वास है कि इस पोस्ट को अच्छे से पढ़ने के बाद आपको शंकु से सम्बंधित किसी प्रश्न को हल करने में कोई दिक्कत नहीं होगी। आप आसानी से Shanku के प्रश्नों को हल कर पाएंगे।
अगर आपको हमारी यह पोस्ट अच्छी लगे तो इसे अपने दोस्तों के साथ शेयर जरूर करें। अपना कीमती समय देने के लिए आपका बहुत – बहुत धन्यवाद।