घन और घनाभ में अंतर, परिभाषा, फॉर्मूला एवं ट्रिक्स | Cube And Cuboid In Hindi

दोस्तों आज का हमारा लेख गणित के महत्वपूर्ण अध्य्याय घन एवं घनाभ ( Cube And Cuboid In Hindi ) से संबंधित होने वाला है। इस लेख में हमने घन एवं घनाभ के बीच के अंतर को समझाने का प्रयास किया है।

हमने इस लेख के माध्यम से आपको घन एवं घनाभ ( Cube And Cuboid ) से संबंधित सभी नियम एवं ट्रिक्स जैसे कि – घन क्या है?, घनाभ क्या है?, घन एवं घनाभ के गुणधर्म क्या होते हैं?, इनके आयतन क्या है? घन एवं घनाभ के महत्वपूर्ण फार्मूला तथा घन एवं घनाभ से संबंधित कुछ प्रश्न इत्यादि विषयों के बारे में बताया है।

उदाहरण सहित इन सब चीजों की जानकारी आपको मिलने वाली है। तो Ghan Aur Ghanabh ( Cube And Cuboid In Hindi ) इस टॉपिक को अच्छी तरह समझने तथा इसके ऊपर अपनी अच्छी पकड़ बनाने के लिए आप सभी इस पोस्ट को अंत तक जरूर पढ़ें।

ताकि आपको घन एवं घनाभ ( Ghan Or Ghanab ) से संबंधित प्रश्नों को हल करने में कोई समस्या न हो तथा आप आसानी से इनके प्रश्नों को हल कर पाएं।
तो आइए जानते हैं –

घन क्या होता है – Ghan Kya Hota Hai

वह ठोस तीन आयाम वाली आकृति जिसकी लंबाई, चौड़ाई और ऊंचाई आपस में समान हो, उस ठोस आकृति को “घन” कहते हैं।

जैसे- लूडो की ‘Dice’, इसकी लंबाई, चौड़ाई एवं ऊंचाई समान होती है, इसलिए यह एक घन का उदाहरण हैं।

अर्थात, ऐसी ठोस आकृति जो छः समान फलको (Face) द्वारा घिरा होता है, उसे ‘घन’ कहते हैं। एक घन में 6 फलक, 8 कोने और 12 किनारे होते हैं।

इसे भी पढ़ें:- वर्ग और वर्गमूल कैसे निकालें?

घनाभ किसे कहते हैं – Ghanab Kya Hota Hai

वह ठोस तीन आयाम वाली आकृति जो छः आयताकार फलको द्वारा घिरी होती है, उसे घनाभ कहते हैं।

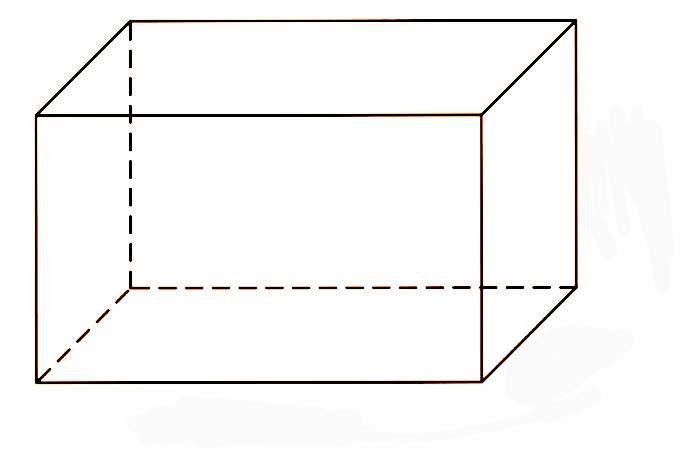
जैसे- माचिस का डिब्बा, किताब आदि के सभी फलक यानी Face आयताकार होती है, इसलिए यह एक घनाभ का उदाहरण है। एक घनाभ में भी 6 फलक, 8 कोने और 12 किनारे होते हैं।

घन एवं घनाभ के गुणधर्म – Properties Of Cube And Cuboid In Hindi

घन के गुणधर्म – Properties of Ghan

• एक घन का आकार लूडो के एक ‘डाइस’ के समान होती है।
• एक घन में ‘6’ फलक होते है और सभी फलक वर्गाकार होते हैं। घन के फलक को ‘घन का सतह’ भी कहा जाता है।
• एक घन में शीर्ष यानी कोने की संख्या आठ होती है। जहां घन की तीन रेखाएं मिलती है, वहां एक शीर्ष का निर्माण होता है। जिसे इंग्लिश में ‘Vertex’ कहते हैं।
• किनारे यानी Edge की बात करें तो एक घन में 12 किनारे होते है और सभी किनारों की लंबाई आपस में समान होती है।
• 4 विकर्ण की संख्या और 24 शीर्षकोणो की संख्या एक घन में पायी जाती है।

इसे भी पढ़ें:- समानुपात क्या होता है तथा समानुपात कैसे निकालें?

घनाभ के गुणधर्म – Properties of Ghanabh

• एक घनाभ का आकार एक किताब एवं माचिस का डिब्बा के आकर सामन होती हैं।
• घनाभ की लंबाई,चौड़ाई एवं ऊंचाई आपस में समान नहीं होती है।
• इसके सभी फलक अर्थात सतह आयताकार आकृति की होती है।
• एक घनाभ में, घन की तरह ही 6 फलक, 8 कोने और 12 किनारे होते हैं।
• इसके सभी कोण 90 डिग्री अर्थात समकोण होते हैं।
• घनाभ में विकर्ण की संख्या 4 होती है।

घन एवं घनाभ का आयतन – Cube And Cuboid Volume In Hindi

घन का आयतन – Ghan Ka Aaytan

घन का आयतन = भुजा×भुजा×भुजा
= (भुजा)³
किसी घन का आयतन ( Ghan Ka Volume ) निकालने के लिए उसके भुजा को तीन बार गुना करने पर जो गुणनफल प्राप्त होता है, वह उसका आयतन कहलाता हैं।

घनाभ का आयतन – Ghanabh Ka Volume

घनाभ का आयतन = l × b × h

जहां, length = लंबाई
breath = चौड़ाई
height = ऊंचाई
किसी घनाभ का आयतन निकालने के लिए उसके लंबाई, चौड़ाई और ऊंचाई को आपस में गुणा करने पर जो गुणनफल प्राप्त होता है, वह उसका आयतन कहलाती है।

घन एवं घनाभ के महत्वपूर्ण फॉर्मूला – Ghan Or Ghanabh Ka Formula

यहां आपको घन ओर घनाभ के सभी महत्वपूर्ण सूत्र ( Cube And Cuboid Formula In Hindi ) मिलेंगे जो आपकी काफी मदद करेंगे।

घन का पृष्ठीय क्षेत्रफल – Ghan Ka Prasthiy Kshetrafal

घन का पूर्ण पृष्ठीय क्षेत्रफल = सभी छः फलकों के क्षेत्रफल का योग
= 2 ( a² + a² + a² )
= 2 × 3a²
= 6a² जहां, a = भुजा

किसी घन का पूर्ण पृष्ठ क्षेत्रफल निकालने के लिए उसके भुजा के स्क्वायर को 6 से गुना करने पर जो गुणनफल प्राप्त होगा, वही उसका पूर्ण पृष्ठीय क्षेत्रफल कहलाएगा।

इसे भी पढ़ें:- वेग किसे कहते हैं तथा वेग कैसे ज्ञात किया जाता है?

घनाभ का पृष्ठीय क्षेत्रफल – Ghanabh Ka Prasthiy Kshetrafal

घनाभ का पूर्ण पृष्ठीय क्षेत्रफल = इसके फलको का कुल क्षेत्रफल
= 2 (लं०×चौ०+चौ०×ऊं०+लं०×ऊं०)
= 2 ( lb + bh + lh)

किसी घनाभ का पूर्ण पृष्ठीय क्षेत्रफल निकालने के लिए उसके फलको के कुल क्षेत्रफल को 2 से गुना करने पर जो गुणनफल प्राप्त होगा, वही उसका पूर्ण पृष्ठीय क्षेत्रफल कहलायेगा।

घन का वक्र पृष्ठीय क्षेत्रफल – Ghan Ka Vakra Prasthiy Kshetrafal

घन का वक्र पृष्ठीय क्षेत्रफल =
= 4 × भुजा × भुजा
= 4 × भुजा²

किसी घन का वक्र पृष्ठीय क्षेत्रफल निकालने के लिए उसके भुजा के स्क्वायर को 4 से गुना करने पर जो गुणनफल प्राप्त होता है, वही उसका वक्र पृष्ठीय क्षेत्रफल कहलाता हैं।

घनाभ का वक्र पृष्ठीय क्षेत्रफल – Ghanabh Ka Vakra Prasthiy Kshetrafal

घनाभ का वक्र पृष्ठीय क्षेत्रफल =
= 2 × ऊंचाई ( लंबाई + चौड़ाई)
= 2 × h ( l + b)

किसी घनाभ का वक्र पृष्ठीय क्षेत्रफल निकालने के लिए उसके लंबाई और चौड़ाई को जोड़कर उसकी ऊंचाई और 2 से गुना करने पर जो गुणनफल प्राप्त होता है, वही उसका वक्र पृष्ठीय क्षेत्रफल कहलाता है।

घन के विकर्ण का सूत्र – Ghan Ka Vikarn Formula

घन का विकर्ण = √3 × भुजा

कई बार जब घन का विकर्ण निकालने की बात आती है तब हम असमंजस में पड़ जाते है कि Ghan ka vikarn kaise nikale| घन का विकर्ण ज्ञात करने के लिए उसके भुजा को रूट 3 से गुणा करने पर जो गुणनफल प्राप्त होता है, वही उसका विकर्ण कहलाता हैं।

घनाभ का विकर्ण कैसे निकालें – Ghanabh Ka Vikarn

घनाभ का विकर्ण =
= √लंबाई² + √चौड़ाई² + √उंचाई²

इसी प्रकार घनाभ का विकर्ण ज्ञात करने के लिए लंबाई, चौड़ाई एवं ऊंचाई को जोड़कर उनके योगफल का वर्गमूल निकाल लें वही उसका विकर्ण ( cuboid ka vikarn ) कहलाएगा ।

घन और घनाभ के कुछ सवाल – Cube And Cuboid Examples In Hindi

Q.1. यदि किसी घन की प्रत्येक भुजा 10 सेंटीमीटर है, तो उसका आयतन क्या होगा ?

हल:- घन की प्रत्येक भुजा = 10 cm

सूत्र से, घन का आयतन = (भुजा)³

         = (10)³ 
         = 10 × 10 × 10
         = 1000 cm³ ans.

Q.2. यदि किसी घन का आयतन 27 cm³ हो, तो घन की प्रत्येक भुजा ज्ञात करें।

हल:- घन का आयतन = 27 cm³

सूत्र से, घन का आयतन = (भुजा)³

         →    27   =  (भुजा)³
         →   भुजा  =   ³√27     अतः घन की प्रत्येक भुजा = 3 cm ans.

Q.3. यदि एक घन की प्रत्येक भुजा 4 मीटर है, तो उसका पूर्ण पृष्ठीय क्षेत्रफल निकालें।

हल:- घन की प्रत्येक भुजा = 4 m
सूत्र से,
घन का पूर्ण पृष्ठीय क्षेत्रफल= 6×भुजा²

         = 6 × (4)²
         = 6 × 16 = 96 m² ans.

Q.4. एक घन की प्रत्येक भुजा 10 सेंटीमीटर की है तो उसके विकर्ण की लंबाई ज्ञात करें।

हल:- घन की प्रत्येक भुजा = 10 cm
सूत्र से,
घन का विकर्ण = √3 × भुजा
= √3 × 10
= 10√3 cm ans.

इसे भी पढ़ें:- BODMAS का नियम क्या होता है?

Q.5. यदि किसी घनाभ की लंबाई 4 मीटर, चौड़ाई 3 मीटर तथा ऊंचाई 2 मीटर है, तो उसका आयतन क्या होगा ?

हल:- यहां, घनाभ की लंबाई = 4 m
घनाभ की चौड़ाई = 3 m
घनाभ की ऊंचाई = 2 m दी है। सूत्र से,
घनाभ का आयतन =
= लंबाई × चौड़ाई × ऊंचाई
= 4m × 3m × 2m
= 24 m³ ans.

Q.6. एक घनाभ की लंबाई 5 मीटर, चौड़ाई 3 मीटर तथा ऊंचाई 2 मीटर हो तो, उसका पूर्ण पृष्ठीय क्षेत्रफल ज्ञात करें।

हल:- सूत्र से, घनाभ का पूर्ण पृष्ठीय क्षेत्रफल= =2(लंबाई×चौड़ाई+चौड़ाई×ऊंचाई+लंबाई×उंचाई)

 = 2 (5 × 3 + 3 × 2 + 5 × 2)
 = 2 ( 15 + 6 + 10 )
 = 2 × 31
 = 62 m² ans.

Q.7. एक घनाभ की लंबाई 4 सेंटीमीटर एवं चौड़ाई 5 सेंटीमीटर और आयतन 40 cm³, तो घनाभ का वक्र पृष्ठीय क्षेत्रफल क्या होगा?

हल:- यहां, लंबाई = 4 cm
चौड़ाई = 5 cm एवं
घनाभ की आयतन = 40 cm³ दी है

सूत्र से, घनाभ का आयतन = l × b × h
→ 40 = 4 × 5 × h
→ 40 = 20 × h
→ h = 40/20
→ h यानी ऊंचाई = 2 cm

अब, घनाभ का वक्र पृष्ठीय क्षेत्रफल =
= 2 × h (l + b)
= 2 × 2 (4+5)
= 4 × 9
= 36 cm² ans.

Q.8. यदि एक घनाभ की लंबाई, चौड़ाई एवं ऊंचाई क्रमशः 10cm, 8cm और 6cm हैं, तो इसके विकर्ण की लंबाई ज्ञात करें।

हल:- सूत्र से,
घनाभ का विकर्ण = √l² + √b² + √h²
= √10² + √8² + √6²
= √100+64+36
= √200
= √2×√2×√2×√5×√5
= 5 × 2 × √ 2
= 10√2 cm ans.

निष्कर्ष :- दोस्तों, तो जैसा कि हमने घन एवं घनाभ के बीच के अंतर ( Difference Between Cube And Cuboid In Hindi ) को तथा इनसे संबंधित सभी तथ्य को इस पोस्ट में आपको अच्छी तरह समझाने की कोशिश की है।

आशा करता हूं कि इस पोस्ट Cube And Cuboid In Hindi की जानकारी आप सभी को हेल्पफुल लगी होगी और इसे समझने में कोई परेशानी नहीं आई होगी। अगर ऐसी कोई चीज जो आपकी समझ में न आयी हो तो आप कमेंट बॉक्स में कमेंट कर सकते हैं। हम उन्हें समझाने का पूरा प्रयास करेंगे। धन्यवाद !

इन्हें भी पढ़ें:-

• वृत के सभी सूत्र
• आयत की परिभाषा, सूत्र एवं महत्वपूर्ण तथ्य
• Number System In Hindi
• लाभ तथा हानि के सभी सूत्र

FAQ About Cube And Cuboid In Hindi